它源于指数，却比指数早产几十年，鬼知道它是怎么诞生的！

给我空间、时间及对数，我就可以创造一个宇宙。

众所周知，指数和对数是互逆的关系，那它们两者那个是较先出现的呢？

应该很多人会回答是指数先出现的，因为我们从开始学习对数的时候，就是从指数引导出来的，当时貌似很多人都是：什么鬼，怎么会有这种东西？！

然而，事实是，对数的诞生是先于指数的，那么，它到底是如何产生的呢？（没有指数的指引，对数的诞生无疑是艰难且神奇的。）

关于对数的基本思想，早在公元前3世纪，阿基米德就研究过几个10的连乘积和10的个数之间的关系，即：

0，1，2，3，4，5，……
1，10，10^2，10^3，10^4，10^5，……

阿基米德发现，两个数列存在某种关系，第一个数列的加减关系可以替代第二个数列的乘除关系。不过很遗憾，他发现这个对应关系之后，并没有继续追寻下去。。。

直到16世纪，德国数学家史蒂非（M.Stifel）才重新拾起这个问题，做出了实质性的贡献，并在后来出版的《综合算术》中记录了他的发现。

他研究的两个数列是：
0，1，2，3，4，5，6，7，8……
1，2，4，8，16，32，64，128，256……

史蒂非也发现跟阿基米德一样的结论：第一个数列之间的加减运算与第二个数列之间的乘除运算有一种对应关系，例如：第一个数列中的两个数3、5之和为8，而第二个数列中对应的两个数8、32的乘积256刚好等于2的8次方。

也即是我们后来所说的第一列数是第二列数以2为底的对数，他们之间存在这样的运算关系：2^3×2^5=2^(3+5)。

不过，但是指数概念并没有完善，特别是当时还没有分数指数的认识，最终导致了史蒂非的这项工作无法进行下去。。。
史蒂非在他的《综合算数》中就很遗憾地表示：“关于数列的这些奇妙的性质，可以写成正本的书，然而，现在我们只是仅仅知道这些，真是遗憾得很！”

但是，史蒂非的发现为对数的产生奠定了基础。

在16世纪末至17世纪初的时候，由于自然科学的飞速发展，科学家们经常会遇到庞大的数值计算，因此，改进数字计算方法就成了当务之急。

尤其是在天文学领域，想要计算一个星球的轨道以及研究星球之间的位置关系，就需要对众多数据进行乘、除、乘方和开方运算，又由于数字庞大，有时候为了得到一个精确的结果，可能会要运算几个月的时间。。。

这时，数学家们就开始寻求简化的计算方法了。

1550年，纳皮尔生于苏格兰爱丁堡的一个贵族家庭。他13岁入圣安德卢斯大学学习，后来留学欧洲，1571年回到家乡。

纳皮尔是一位地主，他曾在自己的田地里进行肥料施肥试验，研究过饲料的配合，还设计制造过抽水机。

他的兴趣十分广泛，一方面热衷于政治和宗教斗争，一方面投身于天文学、数学研究。他在球面三角学的研究中有一系列突出的成果。

1594年，苏格兰数学家约翰·纳皮尔（John Napier）为了简化天文问题中的球面三角的计算，从上面提到的两个数列（r^n→n）引发灵感，他也发现了两个数列中的对应关系，并且，在这个基础上，借助直线运动规律和连续的几何量结合继续研究！

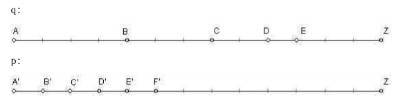
纳皮尔神奇的思路是这样子的（图1）：

首先，他画了两条线，一条是线段AZ，一条是射线A′Z′。

现在，让点q以速度 v₁ 从A出发，沿着AZ作减速运动，速度跟它到Z的距离成比例地递减。

与此同时，点p从A′出发，沿A′Z′作速度为 v₁ 的匀速运动。

即点q在A位置时，对应的p就在A′位置；点q在B位置时，对应的p就在B′位置。

经过不断的研究，纳皮尔发现，q、p两点的运动距离存在着某种对应关系，他把点p到A′的距离称作点q到Z的距离的对数。

即距离A′B′是BZ的对数，A′C′是CZ的对数。

这项简化天文学研究计算量的工作花费了纳皮尔整整20年的时间，而当时没有完善的指数概念，更没有指数符号，所以，并没有“底”的概念，纳皮尔就把对数称为“人造的数”，他创造的“对数”（logarithm）原意是指“比的数”。后人称为纳皮尔对数：Nap.logX。

1614年，纳皮尔出版了名著《奇妙的对数定理说明书》，首次向世人详细说明了对数的概念、运算规律，其中，就包含一个以1-10^(-7)为底的对数表，称为“珍奇对数表”。

"看起来在数学实践中，最麻烦的莫过于大数字的乘法、除法、开平方和开立方，计算起来特别费事又伤脑筋，于是我开始构思有什么巧妙好用的方法可以解决这些问题。"

有趣的是，瑞士力学家、钟表技师比尔吉从1603年开始，用了8年时间，到1611年终于制作出世界上第一个对数表，然而，他选择留以己用，没有发表。。。

直到1620年，在开普勒的恳求下，比尔吉才将它发表出来，称为“算术级数和几何级数表”，然而，这时纳皮尔的对数已经被广泛接受，火遍欧洲。

1616年，纳皮尔的好友布里格斯(H.Briggs)来到爱丁堡看望纳皮尔，对对数给予了很多宝贵的意见，例如：使1的对数为0，10的对数为1等。

不过，第二年，纳皮尔就去世了，布里格斯只好独立完成了对数表的改进，并于1624年出版了《对数算术》，发表了第一张常用对数表。（以10为底包含1~20000及90000~100000的14位常用对数表，符号为lg）

对数的出现，对当时的社会发展起到了重要的影响，大大地简化了天文学、力学的繁难计算。不到一个世纪，就传遍了整个世界，成为必不可少的计算工具。天文学家对于这一发明几乎是欣喜若狂的！

伽利略就曾说：“给我时间，空间和对数，我可以创造出一个宇宙！”

拉普拉斯也说：对数，用缩短计算的时间来使天文学家的寿命延长了数倍。

在1648年，对数经波兰的穆尼斯和中国的薛凤祚合著的《比例与对数》而传入中国。清代数学家戴煦据此发展出很多求对数的简便方法，先后发表了《对数简法》、《续对数简法》、《假数测圆》等著作，这些都是让英国数学家艾约瑟大加赞叹的作品！

到1748年，欧拉在他出版的著作《无穷小分析寻论》中明确指出"对数源于指数"，首先使用y=a^x（a>0，且a≠1）来定义x=log (a) y （a>0，且a≠1）。

1971年，尼加拉瓜发行了一套关于世界上“十个最重要的数学公式”的纪念邮票，每张邮票都于显著位置标出一个重要公式，并配有例子，反面还有公式的简要说明。其中有一张邮票显示的就是纳皮尔发现的对数。

而对数的发明与解析几何、微积分，被公认为17世纪数学的三大成就。